Gravitationsmotor

Gravitationsmotor Semo - eine Studie

Mein Dank an Freund und Mitstreiter Friedhelm, der mir einen interessanten Link zu einem Open Source Projekt Gravitationsmotor geschickt hatte. Ich gebe den Text mit Grafiken (ohne Berichtigung von Deutschfehlern) hier als Original kopiert wieder, da der Entwickler, ein Syrer, um Verbreitung in der Öffentlichkeit bittet.
In der Hoffnung, dass der eine oder andere Maschinenbauer, Techniker, Ingenieur oder Tüftler diese Ideen aufgreift und die Technik zur Vollendung entwickelt. Weitere Erklärungen und Kontakte-mail des Entwicklers finden Sie unten im Text.

Gravitationsmotor Semo

Syrien, Afrin, 2016

Einführung:

Der alte Mensch kämpfte für die Erhaltung seines Lebens und die Gewinnung von genügender Nahrung. Nach der Entdeckung des Feuers sorgte er zusätzlich für die Erzeugung von Energie. Dafür holzte er die Wälder ab, was große Auswirkungen auf das ökologische System der Erde hatte. Das war aber nichts gegen das, was folgte. Für die Erzeugung von mehr Energie plünderte der Mensch den “grünen” Planeten vollständig aus. Die Folgeschäden durch die Förderung und Ausnutzung von Steinkohle, Erdöl und Kernenergie sowie der Entsorgung ihrer Abfälle sind unvorstellbar.

Gravitationsmotor Semo (GMS) stellt eine neue Methode zur Gewinnung von Energie vor. Es ist eine Erfindung mit einer einfachen und einmaligen Konstruktion. Es nutzt die Erdgravitation zur Erzeugung von Drehbewegung aus. Es können Motoren der Leistung von 10, 100, 1000... kW gebaut werden. Damit sind fast alle Probleme der Energieversorgung gelöst.

GMS ist umwelt freundlich, da es keine Abgase, Strahlen oder Abfälle jeglicher Art erzeugt. Es ist zudem geräuschlos und schadet seiner Umgebung nicht. In seiner Nähe hören wir nur das sanfte Pfeifen der Kugellager und das Wehen des Windes beim Fliegen der Gravitationsmassen.

Werden wir jetzt unseren Planeten schonen?
Fast alle Modelle von Gravitationsmotoren benutzen das Ein-Achsen-System. Die Gravitationsmassen werden bei ihrer "Drehung" durch komplizierte und unpraktische Mechanik bewegt, um das Hantelarm auf einer Seite der y-Achse länger als auf der andern Seite zu machen oder die Länge des Hebelarms zu veränderen. Es "entsteht" ein kleines Drehmoment. Dieses Drehmoment kann im besten Fall kaum das Modell in Bewegung setzen. Dazu gehöhrt auch das Bessler-Rad.

Zum ersten Mal wird das Zwei-Achsen-System durch GMS benutzt. Die erste Achse liegt im Ursprung 0 (Hauptachse oder Kraftachse). Die zweite Achse ist paralell zur ersten und liegt in M (Massen-Achse). Beide Achsen sind um R von einander verschoben, (s. gms-GIF). Demnach kann das Motor mit einfacher Mechanik leicht realisiert werden.

Die folgende Studie behandelt diese Methode. Dabei ist das Hauptinstrument des Motors die Hantel
im 1. Bauweg (Bild 1, 3) und das Hebel im 2. Bauweg (Bild 4).

Der Hantel-Schwerpunkt SP mit der Masse SPM = m wird auf den Führungskreis Km geführt, Bild (1). Dieser Kreis, mit dem Mittelpunkt M, hat den Radius R. M liegt im Punkt (R , 0) [Wenn M im Punkt (- R, 0) liegt, kehrt sich nur die Drehrichtung um]. Der Kreis Km berührt die y-Achse in (0, 0), wo die Drehachse liegt. Das Hantelarm schiebt sich in der Drehachse hin und her. Dies geschieht, weil die Bewegung der Hantel eine Drehbewegung mit veränderlichem Radius ist.

Bei der Betrachtung von Bild (1) sehen wir, daβ das Hantelarm auf der positiven Seite der x-Achse immer länger ist, als auf der negativen Seite. Dies entsteht wegen der Führung von SP auf Km. Gerade das ist der Grund für die Entstehung eines Drehmoments. Dieses Drehmoment bewirkt eine rechte Drehung der Drehachse um den Koordinatenursprung 0.

Somit gewinnen wir Energie aus der Gravitation der Erde!
Die Radiuslänge des Schwerpunktes SP ist der Wirkradius r(φ) des Dreh-moments. Die Länge von r(φ) ist die Strecke vom Ursprung 0 bis zum SP. Sie hängt vom Winkel φ(t) ab, Bild (1). Das entstehende Drehmoment wirkt auf den Ursprung 0, da r(φ) in 0 drehbar gelagert ist. Der Wirkradius r(φ), mit beliebigem R, wird wie folgt berechnet:

r(φ) = 2.R.cosφ.............................................[m], φ є {л/2, 0, - л/2}, 2.R ≥ r(φ) ≥ 0...(2)
       (= 2.R.cosφ.er + 0.eφ + 0.ez)
       (= 2.R.cos2φ.ex + 2.R.cosφ.sinφ.ey + 0.ez)

Im Folgenden wird auf die Einführung der Koordinaten verzichtet, weil sie nichts zum bessern Verständnis der Studie bringen. Sie führen nur zu unübersichtlichen und komplizierten Gleichungen. Die Achse in 0 (0-Achse) dreht sich mit der Winkelgeschwindigkeit ω = ω0. Die Achse in M (M-Achse) dreht sich mit der Winkelgeschwindigkeit ωM. Die Drehung um M ist eine Scheindrehung beim 1. Bauweg und echte Drehung beim 2. Bauweg. Bei unseren späteren Berechnungen werden wir mehrmals "Drehung um M" und "Drehung um 0" erwähnen. Eine volle Drehung der M-Achse entspricht in der Wahrheit eine halbe Drehung der 0-Achse. Wir sehen, daβ bei einer vollen Drehung der Hantel um 0 (Drehung um φ = 2.л), SP oder r(φ) zwei volle Drehungen um M (zwei Drehungen um
φ = л) durchführen. Es folgt demnach:
ω = ω0 = ωM/2...............................................[rad/s]....................................................(3)

Alle Gröβen wirken auf die 0-Achse und werden von ihr entnommen oder an ihr gemessen. Es ist zu beachten, daβ der Wirkradius r(φ) bei seiner Drehung auf Km, sich nur auf der positiven Seite der x-Achse bewegt!

Nun betrachten wir die Drehung der Hantel als Ganzes:
rmi(φ) ist der veränderliche Radius der einzelnen Hantelmassen mi bei ihrer Drehung um den
Ursprung 0. Es ist mit ℓ = 4.R, Bild (1) und Gl (2, 7):
rmi(φ) = ℓ + 2.R.cosφ.....................................φ є {0, 2л}, 6.ℓ ≥ rmi ≥ 2.ℓ.....................(4)
rm1(φ) = ℓ + 2.R.cosφ...................................φ є {л/2, 0, - л/2}, 6.ℓ ≥ rm1 ≥ 4.ℓ.....(4 - a)
rm2(φ) = ℓ - 2.R.cosφ....................................φ є {- л/2, л, л/2}, 4.ℓ ≥ rm2 ≥ 2.ℓ.....(4 - b)

rm1(φ) ist der Radius (0 - mi) auf der positiven Seite der x-Achse. rm2(φ) ist der Radius (0 - mi) auf der negativen Seite der x-Achse. Beide Radien, da sie der selben Hantel gehören, entstehen von einander bei der Drehung um φ = л. Es folgt für die Differenz beider Radien rmd(φ), Gl (4):
rmd(φ) = rm1(φ) - rm2(φ) = (ℓ + 2.R.cosφ) - (ℓ - 2.R.cosφ)
rmd(φ) = 4.R.cosφ = 2.r(φ)...........................φ є {л/2, 0, - л/2}..................................(5)

Aus dieser Gleichung folgt, daβ der Wirkradius r(φ) und somit das Drehmoment, von der Länge ℓ und demnach von der Länge des Hantelarms unabhängig ist!
Es genügt also nur die Bewegung des Hantel-Schwer-Punktes zu studieren!

Eine wunderbare Entdeckung:

Schauen wir nun die Gl (4) sowie den Verlauf der beschriebenen Kurve durch die Hantelmassen im Bild (1) genau an. Beim Nachschlag der Seite 86 von Bronstein*, stellen wir mit gröβter Überraschung fest, Bild (2):

Die durch die Hantelmassen beschriebene Kurve, ist nichts anderes als die PASCAL-SCHNECKE!

In beiden Varianten können beliebige Hantel, mit nur einer Achse und zwei Lagerträger, gebaut werden. Die Verschiebung der Hantel gegen einander wird von der Konstruktion der Drehachse gewährleistet. Es entsteht eine zentrifugale Kraft in der positiven Richtung der x-Achse.

2. Bauweg:

Hier ist das Hebel das Hauptinstrument des Motors mit der Hebelarm-Länge r(φ). Dieser Bauweg beruht auf die Bewegung von Massenpunkten auf den Kreis Km. Sie sind die Gravitationsmassen GM. Wir haben demnach mit Hebeln und GM statt mit Hanteln und ihrer Schwerpunkten SP zu arbeiten. Somit reduziert sich die Motorgöβe zur Hälfte, Bild (4). Bei diesem Bauweg ist R frei von den Beschränkungen der Gln (6 + 7), d.h. unabhängig von der Hantelarm-Länge ℓ. Wir ersparen auch
die komplexe Konstruktion der Drehachse.

Das Motor besteht aus einer Kraftscheibe mit dem Radius (2.R). Sie ist von einer Seite drehbar gelagert. Auf der anderen Seite sind Leitschienen auf ihr befestigt, die gegen einander symmetrisch gedreht sind. Die Zahl der Leitschienen ist gleich die Zahl der GM. Die Kraftscheibe ist gleichzeitig die gewünschte Schwungmasse. Genau gegenüber dem Kreismittelpunkt M wird eine zweite Achse,
parallel zur Ersten, gestellt. Sie ist die M-Achse. Sie wird von der Außenseite auf einem Halter befestigt. Auf dieser Achse von Innen drehen sich die GM. Sie drehen sich völlig frei von einander. Verbindungsarme werden in den Schwerpunkten der GM, befestigt (im Bild nicht sichtbar). Die Schwerpunkte der GM laufen auf Km. Die anderen Seiten der Verbindungsarme schieben sich in den
Leitschienen hin und her. Es wird auch eine Trommel und ein Führungsrad eingebaut. Die Bahngeschwindigkeit der Trommel von Auβen muβ gleich der Bahngeschwindigkeit der GM von Auβen sein (Statt der Trommel und dem Führungsrad kann auch ein Magnetmechanismus eingeführt werden). Die Verbindungsarme mit den Leit-schienen gewährleisten die symmetrische Verschiebung
der GM gegen einander.

Bei der Drehung der GM, unter dem Einfluss der Gravitationskraft, schieben sich die Verbindungsarme in den Leitschienen hin und her. Bei rechter Drehung drehen die GM im I + II Quartal die Kraftscheibe mit sich (Fallarbeit). Dagegen dreht die Kraftscheibe im III + IV Quartal die GM mit sich (Hubarbeit). Das Drehmoment wird von der Achse der Kraftscheibe entnommen, Bild (5, 6). Die Trommel hebt die GM bei ihrer Drehung im Ursprung mit sich. Somit wird der kritische Punkt im Ursprung 0 überwunden. Die Trommel bekommt ihre Drehbewegung von der Kraftscheibe über den Führungsrad.

Eine Drehung der Kraftscheibe um 0 ergibt zwei Drehungen der GM oder r(φ) um M. r(φ) ist die Strecke vom Verbindungsarm bis zum Ursprung 0. Hier drehen sich die GM tatsächlich um die M-Achse. Sie wirken aber über r(φ) auf die 0-Achse. Es können mehrere Einheiten neben einander mit teilweise gemeinsamen Achsen gebaut werden. Die Kraftscheibe kann von Auβen auf drei gelagerte Räder mit 1200 Verschiebung, statt der Achse 0, gestellt sein, Bild (4). Somit können Leitschienen und Gravitationsmassen auf beiden Seiten der Kraftscheibe gestellt werden. Es entsteht hier keine zentrifugale Kraft.

Abmessungen:

Im Folgenden deutet der Index W1 auf den 1. Bauweg und W2 auf den 2. Bauweg.

1. Bauweg:

Die horizontale Länge Lh,W1 des Motors ist, Bild (1), Gl (4, 7):

Lh,W1 = 2.ℓ = 8.R..........................................................................................................(8)

Die vertikale Länge Lv,W1, die Strecke zwischen den Extremwerten C und D, ist nach Bronstein S 86
und Bild (1):

Lv,W1 ≈ 8,81.R..............................................................................................................(9)

2. Bauweg:

Die horizontale Länge Lh,W2 ist gleich der vertikalen Länge Lv,W2, Bild (4):

Lh,W2 = Lv,W2 = 4.R...................................................................................................(10)

Die Breite Lb,W1 und Lb,W2 des Motors wird durch den Bauweg, die Form und die Zahl der
Hantelmassen oder der GM bestimmt.

Benutzung mehrer Hantel o. Hebel Hz:

Bei der Benutzung mehrerer Hantel oder Hebel müssen sie gegen einander symmetrisch gedreht
sein. Der Verschiebungswinkel φv zwischen den einzelnen Hanteln oder den Wirkradien der
Hebelmassen, mit der Hantel- oder Hebelzahl Hz ist:

φv = л/Hz.....................................................................................................................(11)

Die weiteren Berechnungen für die Hantel sind die selben Berechnungen für das Hebel. Der Wirkradius r(φ) von SP der Hantel ist genau gleich dem Wirkradius r(φ) der Masse GM des Hebels. Deswegen wird im Folgenden, der Einfachheitshalber, nur von Hanteln geredet. Die Hantelzahl Hz ist demnach, mit der Zahl der Grundeinheiten GE, (s.u.: Das Drehmoment):

Hz = 4.(GE)   →   GE = Hz/4..........................GE є N, Hz є 4.N................................(12)

Alle Massen SPi oder GMi sind gleich:

m = mi.............................................................SPMi = GMi = m.................................(13)

Die Masse der Trägheit Θ:

Die Trägheitsmasse** Θ wird wie folgt berechnet:

Zuerst berechnen wir die Trägheitsmasse ΘM,1 einer Hantel bei der Drehung von SP auf den Kreis Km. Danach berechnen wir, nach Steiner**, die Trägheitsmasse Θ0,1 einer Hantel bei der Drehung um den Ursprung 0. Schließlich wird die Träg-heitsmasse mit beliebiger Hantelzahl bei der Drehung um M und 0 berechnet.

Die Trägheitsmasse ΘM,1 einer Hantel mit SPM = m, bezogen auf M, ist:

ΘM,1 = m.R2....................................................Hz = 1.................................................(14)

Nach Steiner, bei der Drehung um einen beliebigen Punkt A, ist die resultierende Trägheitsmasse:

ΘA = m.a2 + Θ............................................................................................................(15)

In unserem Fall liegt der Punkt A im Ursprung 0. Mit dem Abstand a = R, folgt für die Trägheitsmasse
Θ0,1 einer Hantel bei der Drehung um 0:

Θ0,1 = m.a2 + Θ = m.R2 + m.R2 = 2.m.R2.....Hz = 1................................................(16)

Die Trägheitsmasse ΘM = ΘM,Hz mit beliebiger Hantelzahl Hz = 4.(GE), bezogen auf M, ist :

ΘM = ΘM,1.Hz = m.R2.Hz.................................[kg.m2]..............................................(17)

Für die Trägheitsmasse Θ = Θ0,Hz mit Hz = 4.(GE), bezogen auf 0, folgt:
Θ = Θ0,Hz = Θ0,1.Hz = 2.m.R2.Hz...................[kg.m2]...............................................(18)

Das Drehmoment M:

Für die Gravitationskraft** F, mit der Gravitationskonstante g = 9,80665 m/s2, gilt:

F = m.g = - m.g………………………….....…[N = kg.m/s2]………………....………(19)

Alle Hantelmassen mi und somit auch alle Kräfte Fi sind gleich, Gl (13). Alle SPi drehen sich auf den Kreis Km unter dem Einfluβ der Erdgravitation g.

Das Ein-Hantel-Motor:

Die Gravitationskraft F hat eine tangentiale Komponente Ft(φ) auf den Kreis Km. Sie ist die Kraft, die die SP auf den Fϋhrungskreis bewegt. Sie ist, Bild (5) und Gl (19):

Ft(φ) = F.cos2φ = - m.g.cos2φ.................................................................................(20)

Die Kraft Ft(φ) hat ihrerseits eine Komponente Fs(φ) die immer senkrecht auf den Wirkradius r(φ) steht. Die Kraft Fs(φ) bewirkt das entstehende Drehmoment. Dieses Drehmoment wirkt ϋber r(φ) auf den Ursprung 0. Sie ist, Gl (20):

Fs(φ) = Ft(φ).cosφ = - m.g.cos2φ.cosφ..................................................................(21)

Das Drehmoment** M(φ) ist:

M(φ) = r(φ) x Fs(φ) = r(φ) . Fs(φ) . sinφ.................................................................(22)

r(φ) und Fs(φ) stehen immer senkrecht auf einander. Demnach ist sinφ = 1. Es folgt:

M(φ) = r(φ) . Fs(φ)....................................................................................................(23)

Es folgt für das Drehmoment M1(φ) der Kraft F1, Gl (2, 21, 23):
M1(φ) = (2.R.cosφ) . (- m.g.cos2φ.cosφ)

M1(φ) = - 2.R.m.g.cos2φ.cos2φ...................Hz = 1, φ є {л/2, 0, - л/2}....................(24)

Das entstehende Drehmoment M1(φ) dreht von φ = л/4 → φ = 0 → φ = - л/4 den Wirkradius r(φ) oder SP im Uhrzeigersinn. Dagegen dreht das entstehende Drehmoment M1(φ) von φ = л/4 → φ = ± л/2 → φ = - л/4 den Wirkradius r(φ) oder SP gegen das Uhrzeigersinn, [Bild (6) für Hz =1].

Wir haben drei kritische Punkte:

P1 liegt bei φ = л/4, ist eine labile Ruhelage.
P2 liegt bei φ = - л/4, ist eine stabile Ruhelage.
P3 liegt im Ursprung 0. Bei diesem kritischen Punkt verschwindet das Drehmoment, da r(φ) = 0 ist. Es wirkt nur die Schwere-Kraft F = - m.g.

Das Zwei-Hantel-Motor:

Nach Gl (11) ist der Verschiebungswinkel φv = л/2, Bild (5). Der Radius r1(φ) steht senkrecht auf den Radius r2(φ). Das resultierende Drehmoment M1,2(φ) der Kräfte F1 und F2 ist bei der Drehung um M, Gl (24):

M1,2(φ) = - 2.R.m.g.cos2φ.cos2φ - 2.R.m.g.cos2(л/2 - φ).cos2(л/2 - φ)
             = - 2.R.m.g.[cos2φ.cos2φ + cos(л - 2φ).cos2(л/2 - φ)]
             = - 2.R.m.g.[cos2φ.cos2φ + (- cos 2φ).sin2φ]
             = - 2.R.m.g.cos2φ.(cos2φ - sin2φ) = - 2.R.m.g.cos2φ.cos2φ
M1,2(φ) = - 2.R.m.g.cos22φ............................Hz = 2, φ є {л/2, 0, - л/2}..................(25)

Es gibt eine labile Ruhelage bei φ = ± л/4 und einen kritischen Punkt im Ursprung 0.

Das Vier-Hantel-Motor:

Nach Gl (11) ist der Verschiebungswinkel φv = л/4, Bild (5). Die Radien r1(φ), r2(φ), r3(φ) und r4(φ) sind gegeneinander um φv = л/4 verschoben. Das resultierende Drehmoment M1,2(φ) der Kräfte F1 und F2 bei der Drehung um M ist in Gl (25) berechnet. Da r3(φ) und r4(φ) senkrecht auf einander stehen, ist das resultierende Drehmoment M3,4(φ) der Kräfte F3 und F4 bei der Drehung um M, Gl (24)
und Bild (5):

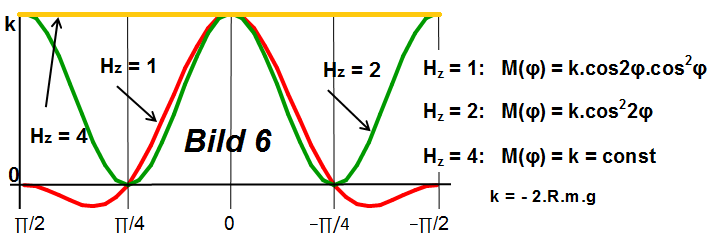
In vektorieller Schreibweise folgt für das Drehmoment in Gl (29), da das entstehende Drehmoment
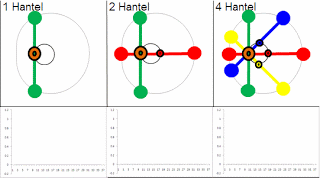
M(φ) eine rechte Drehung bewirkt, mit Hz = 4.(GE) und Bild (5):

M(φ) = - R.m.g.Hz.ez = const.........................φ є {л/2, 0, - л/2}...............................(30)

Die Arbeit W_tr und W_rot:

Die Translationsarbeit W_tr:

Alle SPi leisten Translationsarbeit** Wtr(φ) bei ihrer Drehung auf den Kreis Km. Jeder SPi leistet Hubarbeit von
φ = - л/4 → φ = ± л/2 → φ = л/4

dagegen Fallarbeit von

φ = л/4 → φ = 0 → φ = - л/4

Die Translationsarbeit Wtr(φ) für eine volle Drehung der SPi auf den geschlossenen Weg Km ist:

∑ Wtr(φ) = 0................................................................................................................(31)

Die Rotationsarbeit W_rot:

Die Rotationsarbeit** W_rot ist:

W_rot = ∫ M(φ).dφ.........................................................................................................(32)

Die Rotationsarbeit Wrot,M bei der Drehung um M ist, Gl (28, 32):
                                              - л/2
W_rot,M = (- R.m.g.Hz/2). ∫ dφ...........................φ є {л/2, 0, - л/2}...............................(33)
                                              + л/2
Es folgt nach der Integration* (volle rechte Drehung um M):
                                                - л/2
W_rot,M = (- R.m.g.Hz/2).φ|   + C.................................................................................(34)
                                               + л/2
Die Integrationskonstante C wird wie folgt berechnet:

r(± л/2) = 0 => MM(± л/2) = 0 => W_rot,M(± л/2) = 0 => C = 0.............................(35)

Wir erhalten für W_rot,M bei der Drehung um M:

W_rot,M = (- R.m.g.Hz/2).[(- л/2) - (+ л/2 )] = (- R.m.g.Hz/2).(- л)

W_rot,M = л.R.m.g.Hz/2 = const…………....…[Nm = kg.m2/s2].................................(36)

Wir erhalten für W_rot= W_rot,0 bei der Drehung um 0, nach der Multiplikation der Gl (36) mit 2, da zwei Drehungen um M eine Drehung um den Ursprung 0 ergeben. Die Rotationsarbeit bei der Drehung um 0 ist demnach die Doppelte als um M. Es folgt:

Wrot = 2.(л.R.m.g.Hz/2)

Wrot = л.R.m.g.Hz = const…………………..[Nm = kg.m2/s2]..................................(37)

Die Winkelgeschwindigkeit ω:

Die Rotationsenergie** E_rot ist:

E_rot = Θ.ω2/2..............................................................................................................(38)

Das Drehmoment MM(φ) und die Rotationsarbeit Wrot,M wurden für die Drehung um M berechnet, Gl (28, 36). Dann wurden beide Gleichungen mit dem Faktor 2 multipliziert, um die Werte von M(φ) und Wrot für die Drehung um 0 zu erhalten, Gl (29, 37). Nun berechnen wir weiter, aber für jeden Bauweg getrennt:

1. Bauweg:

Die Rotationsenergie Erot,W1 = Erot,0,W1 entsteht von der Drehung der einzelnen Hantel um 0. Es folgt deswegen, Gl (18, 38):

E_rot,W1 = 2.m.R2.Hz.(ωW1)2/2........................[Nm = kg.m2/s2]................................(39)

Die Rotationsarbeit W_rotdes Drehmoments ist nach dem Energie-Erhaltungs-Satz der Mechanik** gleich der Rotationsenergie E_rot. Dabei wurde die Reibung vernachläβigt. Mit Epot = W_tr = 0, folgt bei der Drehung um 0, Gl (37, 39):

W_rot,W1 = л.R.m.g.Hz = 2.m.R2.Hz.(ωW1)2/2 = Erot,W1

(ωW1)2 = (л.R.m.g.Hz)/(m.R2.Hz) = (л.g)/R

Es folgt für die Winkelgeschwindigkeit** ωW1 = ω0,W1 bei rechter Drehung um 0:

ωW1 = - |√(л.g/R)| = const…………………..[rad/s]..................................................(40)

ωW1 ≈ - 5,55/|√R|......................................................................................................(41)

Es folgt in vektorieller Schreibweise für Gl (40) bei rechter Drehung um 0:

ωW1 = - |√(л.g/R)|.ez = const……………....[rad/s]..................................................(42)

2. Bauweg:

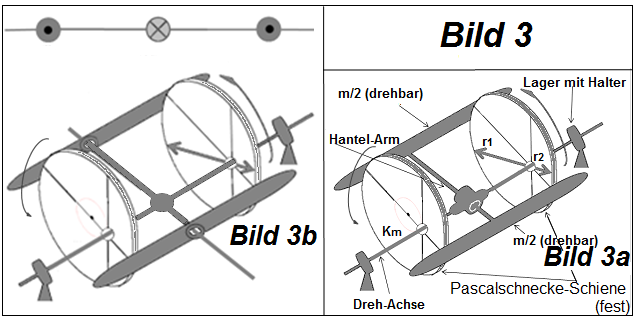
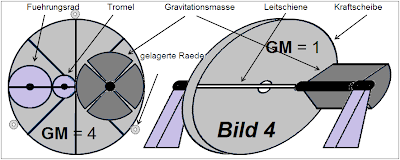
Die Rotationsenergie Erot,M,W2 entsteht von der Drehung der einzelnen GM um M. Sie wirkt über die Verbindungsarme und die Leitschienen auf die Kraftscheibe und demzufolge auf die 0-Achse. Es folgt deswegen, Gl (17, 38):

Erot,M,W2 = m.R2.Hz.(ωM,W2)2/2.....................[Nm = kg.m2/s2]................................(43)

Es folgt mit Gl (36, 43):

Wrot,M,W2 = л.R.m.g.Hz/2 = m.R2.Hz.(ωM,W2)2/2 = Erot,M,W2

(ωM,W2)2 = (л.R.m.g.Hz/2)/(m.R2.Hz/2) = (л.g)/R

ωM,W2 = - |√(л.g/R)| = const……………………………..…………………...………(44)

Es folgt für ωW2 bei der Drehung um 0, Gl (3, 44):

ωW2 = - |√(л.g/R)|/2 = ωW1/2 = const...........[rad/s].................................................(45)

ωW2 ≈ - 2,78/|√R|......................................................................................................(46)

Es folgt in vektorieller Schreibweise für Gl (45) bei rechter Drehung um 0:

ωW2 = - |√(л.g/R)|/2.ez = const.....................[rad/s].................................................(47)

Die Rotationsleistung Prot:

Die Rotationsleistung** Prot ist:

Prot = M(φ).ω(φ).......................................................................................................(48)

1. Bauweg:

Das Drehmoment und die Winkelgeschwindigkeit sind konstante Werte, Gl (29, 40). Die Rotationsleistung Prot,W1 = Prot,0,W1 bei der Drehung um 0 ist, Gl (29, 40, 48):

Prot,W1 = M.ω.............................................................................................................(49)

Prot,W1 = (- R.m.g.Hz).[- |√(л.g/R)|]

Prot,W1 = (m.Hz).|√(л.R.g3)|............................[W = kg.m2/s3]..................................(50)

Prot,W1 ≈ 54,43.m.Hz.|√R|.........................................................................................(51)

2. Bauweg:

Das Drehmoment und die Winkelgeschwindigkeit sind hier auch konstante Werte, Gl (28, 45). Es folgt demnach für die Rotationsleitung Prot,M,W2 bei der Drehung um M, Gl (28, 45, 48):

Prot,M,W2 = MM.ωM………………………………………...………………………….(52)

Prot,M,W2 = (- R.m.g.Hz/2).[- |√(л.g/R)|]

Prot,M,W2 = (m.Hz).|√(л.R.g3)|/2................................................................................(53)

Es folgt für Prot,W2 = Prot,0,W2 = 2.Prot,M,W2, da die Rotationsleistung bei der Drehung um 0, die doppelte als um M ist, Gl (53):

Prot,W2 = 2.[(m.Hz).|√(л.R.g3)|/2]

Prot,W2 = (m.Hz).|√(л.R.g3)| = Prot,W1............[W = kg.m2/s3]..................................(54)

Prot,W2 ≈ 54,43.m.Hz.|√R|.........................................................................................(55)

Die Drehzahl n:

Es ist:

ω = 2.л.f   →   f = ω/(2.л)...........................................................................................(56)

n = 60.f........................................................................................................................(57)

1. Bauweg:

Die Frequenz** fW1 = f0,W1, der 0-Achse, wird wie folgt berechnet, Gl (56):

fW1 = ωW1/(2.л)..........................................................................................................(58)

Mit Gl (40, 58) folgt für die Frequenz fW1:

fW1 = [- |√(л.g/R)|]/(2.л)

fW1 = - |√[(g/(л.R)]|/2 = const.........................[Hz = 1/s]...........................................(59)

fW1 ≈ - 0,883/|√R|......................................................................................................(60)

Die Drehzahl** nW1 = n0,W1 der 0-Achse ist, Gl (57):

nW1 = 60.fW1..............................................................................................................(61)

Mit Gl (59, 61) folgt für die Drehzahl nW1:

nW1 = 60.{- |√[(g/(л.R)]|/2}

nW1 = - 30.|√[g/(л.R)]| = const.......................[U/Min]................................................(62)

nW1 ≈ - 53/|√R|...........................................................................................................(63)

2. Bauweg:

Die Frequenz fW2 = f0,W2 der 0-Achse wird wie gefolgt berechnet, Gl (45, 56):

fW2 = - [|√(л.g/R)|/2]/2.л.............................................................................................(64)

fW2 = - |√(g/л.R)/4| = fW1/2 = const................[Hz = 1/s]..........................................(65)

fW2 = - 0,442/|√R|......................................................................................................(66)

Mit Gl (57, 65) folgt für die Drehzahl nW2:

nW2 = 60.[- |√(g/л.R)|/4].............................................................................................(67)

nW2 = - 15.|√[g/(л.R)]| = nW1/2 = const..........[U/Min]...............................................(68)

nW2 = - 26,5/|√R|.......................................................................................................(69)

Die Gl (45, 65, 68) besagen: ωW1, fW1 und nW1 beim 1. Bauweg haben das doppelte Wert als ωW2, fW2 und nW2 beim 2. Bauweg! Dies ist Konsequenz der Gln (4 + 5). Beim 1. Bauweg ist der Radius der einzelnen Hantelmassen länger als der Radius der Hebelmasen, Bild (1, 3, 4). Dies bewirkt gröβere Bahn- und Winkel-Geschwindigkeit, und demzufolge gröβere Frequenz und Drehzahl.
Die Rotationsleitung Prot in beiden Bauwegen ist gleich und muβ gleich sein, Gl (50, 54). Es folgt somit:

Prot = Prot,W1 = Prot,W2 = (m.Hz).|√(л.R.g3)|.....[W = kg.m2/s3]...............................(70)

Prot ≈ 54,43.m.Hz.|√R|...............................................................................................(71)

Die Reibung R:

Die Reibungsleistung** PR wird von der Rotationsleistung Prot dividiert. Die Reibungsleistungen sind im Einzelnen:

Pk der Kugellager (Achsen, Verbindungsarme, Zahnräder, Trommel),

Pz der Zahnräder,

Pt   zwischen Gravitationsmassen und Trommel,

Pl   Luftwiderstand beim drehen der Hantel- oder Gravitationsmassen.

Es folgt für die Gesamtleistung Pg:

Pg = Prot - PR = Prot - (Pk + Pz + Pt + Pl)……………………………………...…….(72)

Die Berechnung jeder Reibungsart kann nur an konkret bestimmten Motoren berechnet werden. Erst dann werden die Zahl und Art der Kugellager, die Gröβe der Trommel, die Form und Gröβe der Zahnräder sowie der GM bestimmt.

Abschluβ:

Die Grundidee der Studie ist: Einführung des Zwei-Achsen-Systems! Das Hantelarm wurde drehbar im Ursprung gelagert und der Schwerpunkt auf den Kreis Km gedreht. Dann übergingen wir zu Gravitationsmassen, die sich um M drehen und über r(φ) auf den Ursprung wirken. Es entsteht ein Drehmoment. Von der Hauptachse erhalten wir Rotationsarbeit und demzufolge Rotationsleistung. Wir erhalten z.B. von einem 4 x 4 x 4 Meter Raum, der ca. 30 Tonnen Eisen und Beton enthält (weniger als das Gewicht eines Panzers), eine Leistung von 1,7 MW, siehe Tabelle für R = 1 m. Beim GMS gibt es nur bautechnische Obergrenzen für die Leistung. Da haben wir die kostenlose und dauernde Energie in der Hand. Das Motor schont Mensch, Erde, und Atmosphäre.

Es hat außerdem, im Vergleich zu den andern Kraftwerken, nicht erwähnenswerte Bau- und Wartungskosten.
Leistung wurde mit einem einfachen mechanischen Trick von der Gravitation der Erde gewonnen!

Tabelle: Einige theoretisch-berechnete Werte des GMS:

R [m] m [kg] ge Hz nW1 [U/Min] Pge [W] PHz [W]
0.25 250 2 8 106 27 k 54 k
0.5 500 4 16 74 76 k 304 k
1 1000 8 32 53 217 k 1.7 M
2 2000 16 64 37 615 k 9.8 M
4 4000 32 128 26.5 1.7 M 54 M
8 8000 64 256 18.7 4.9 M 313 M

Es ist vieles studiert und probiert worden. Zu einem wirtschaftlich nützlichem und praktisch arbeitendem Modell ist man noch nicht gelangt. Fast alle Modelle, die ich vom Net erhielt, sind technisch-mechanisch kompliziert und nicht effektiv oder schwer realisierbar, weil sie das Ein-Achsen-System benutzen. Mein Modell (vorallem der 2. Bauweg), so glaube ich, ist technisch-mechanisch praktisch und einfach realisierbar.

Ich konnte leider mein Labormodell (1. Bauweg) nicht zu Ende führen, das mir die "Richtigkeit" der Studie bestätigte. Nach Einbeziehung Aleppos in den Krieg (2012) muβte ich die Stadt verlassen. Das Labormodell ist höchstwahrscheinlich samt meinem Haus in die Luft gesprengt worden, da mein Wohngebiet (Saif Al Daulah) das zweite Bermuda-Dreieck geworden ist.

Ich lege hiermit meine Studie der Öffentlichkeit vor. Das Gravitationsmotor muβ zur Wirklichkeit werden und nicht ewiger Wunsch bleiben! Die vorhandenen Versuche, Konstruktionen und Berechnungen sollen von Allen veröffentlicht werden. Somit wird man hoffentlich schnell zum Gravitationsmotor gelangen. Alle, die in diesem Bereich arbeiten, brauchen bestimmt finanziele
Unterstützung. Es soll aber wegen eventeull erwartete finanziele Vorteile nicht auf das Ziel verzichtet werden, wie Bessler, der sein Rad selber zerschlug. 300 Jahre sind somit verloren!

Ich kann momentan wegen der Lage in Syrien, vorallem aus finanzielen Gründen, ein anderes Labormodell nicht bauen. Ich bin gezwungen mich mit dieser thoretischen Studie zu begnügen. Ich werde aber, sobald es mir möglich wird, ein neues Modell bauen und meine Versuche daran durchführen. Sie sind vorallem:

          Leerlauf und Voll-Last,
          Plötzliche Belastung und Entlastung,
          Frequenz bei Änderung der Last,
          Wirkungsgrad des Motors,
          Beschleunigung, schiefe Ebene und Neigung (Autos),
          Schwingungen und Wellen (Schiffe).

Literatur:

*    Bronstein-Semendjajew: Taschenbuch der Mathematik.
** Die bekannten sehr vielen deutschsprachigen Physik-Lehrbücher und Beiträge
     über Massenpunkt und Drehbewegung, die ich vom Net erhielt.

PS:
+      Beiträge, Vorschläge und Kritiken zu dieser Studie werden im Teil Diskussion
        dieser web-Seite, ganz oder Teilweise mit eventeuller Stellungnahme,
        veröffentlicht.
++    Kontakt, Beiträge und Fragen bitte an mein eMail gms.semo@gmail.com
<mailto:gms.semo@gmail.com>           senden.

Widmung:

Meiner Familie und allen Familien im Mittelost gewidmet, die das ungeheuere mit mir
vertragen!

Gravitationsmotor Semo mit seinen zwei Achsen ist leicht zu bauen. Mit einem einfachen mechanischen Trick gewinnt es Energie von der Erdgravitation. Es hat nur bautechnische Obergrenzen für die Leistung. Es können Motoren der Leistung von 10, 100, 1000… kW gebaut werden. Es ist Umwelt freundlich, da es keine Abgase, Strahlen oder Abfälle jeglischer Art erzeugt.
Es darf nicht mehr länger daueren, daβ man zu einem praktisch-arbeitenden und wirtschaftlichen-nützlischen Gravitationsmotor kommt. Da haben wir die kostenlose und dauernde Energie in der Hand. Gravitationsmotoren müssen mit den Bemühungen aller zur Wahrheit werden…

Für mehr klicke (voller Studientext): Gravitationsmotor Semo

محرك الجاذبية سمو ذو المحورين سهل البناء. بخدعة ميكانيكية بسيطة يكتسب طاقة من الجاذبية الارضية. ليس لديه حد علوي للاستطاعة سوى الحدود الإنشائية-الميكانيكية. نستطيع بناء محركات بالاستطاعة 10, 100, 1000... .kW هو صديق للبيئة لانه لاينتج غازات, اشعاعات او نفايات مهما كانت.
لا يجوز ان يطول الزمن حتى نبني محرك جاذبية عملي-عامل واقتصادي-مفيد. هنا لدينا الطاقة الدائمة وبدون كلفة. محرك الجاذبية يجب ان يصبح حقيقة بجهود الجميع...
للمزيد اضغط (النص الكامل للدراسة): محرك الجاذبية سمو

Internetseite: https://sites.google.com/site/gravitymotorsemo/gravitationsmotorsemo

Text und Grafiken: Entwickler

Kommentare, Anregungen, Meinungen zum blog